반응형
예제
힘을 받는 어떤 물체 내부의 한 지점에서 응력상태는 아래와 같습니다. 주응력상태를 나타내세요.

풀이
주응력과 회전각을 계산하는 수식은 아래와 같습니다.
$\tan 2\theta=\frac{\tau_{xy}}{\frac{(\sigma_{x}-\sigma_{y})}{2}}$
$\sigma_{1,2}=\frac{\sigma_{x}+\sigma_{y}}{2}
\pm
\sqrt{\left ( \frac{\sigma_{x}-\sigma_{y}}{2} \right )^{2}+\tau_{xy}^{2}}$
1) 회전각 계산
회전각을 계산해줍니다.
$\tan 2\theta=\frac{3}{4}$
엑셀에 DEGREES(ATAN(3/4)*0.5) 수식을 입력하면 $\theta$를 구할 수 있습니다.
$\theta=18.4^{\circ}$
2) 주응력 계산
주응력을 계산해줍니다.
$\sigma_{1,2}=\frac{100+20}{2}\pm\sqrt{\left ( \frac{100-20}{2} \right )^{2}+30^{2}}$
계산하면 아래와 같습니다.
$\sigma_{1,2}=60\pm50$
$\sigma_{1}$ 과 $\sigma_{2}$ 는 아래와 같습니다.
$\sigma_{1}=110$ , $\sigma_{2}=10$
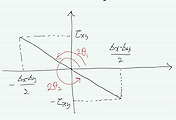
3) 응력 상태
응력상태를 나타내면 아래와 같습니다.

반응형
'재료역학 > 평면응력과 응력 변환' 카테고리의 다른 글
| [재료역학] 평면응력 (6) 모어원 유도 (0) | 2022.06.15 |
|---|---|
| [재료역학] 평면응력 (5) 최대전단응력 예제 1 (0) | 2022.06.15 |
| [재료역학] 평면응력 (3) 최대전단응력공식 유도 (0) | 2022.06.10 |
| [재료역학] 평면응력 (2) 주응력공식 유도 (0) | 2022.06.09 |
| [재료역학] 평면응력 (1) 응력의 변환방정식 유도 (0) | 2022.06.07 |


댓글