[재료역학] 평면응력 (6) 모어원 유도

모어원의 유도는 평면응력의 변형방정식에서 출발합니다. 아래와 같습니다. 

 

$\sigma_{x'}=\frac{\sigma_{x}+\sigma_{y}}{2}+\frac{\sigma_{x}-\sigma_{y}}{2}\cos 2\theta+\tau_{xy}\sin 2\theta$    (1) 

 

$\tau_{x'y'}=-\frac{\sigma_{x}-\sigma_{y}}{2}\sin 2\theta+\tau_{xy} \cos 2\theta$    (2) 

 

1번 식을 아래와 같이 이항합니다. 

 

$\sigma_{x'}-\frac{\sigma_{x}+\sigma_{y}}{2}=\frac{\sigma_{x}-\sigma_{y}}{2}\cos 2\theta+\tau_{xy}\sin 2\theta$

 

위 식의 양변을 제곱해줍니다. 2번식도 양변을 제곱해줍니다. 

 

$\left ( \sigma_{x'}-\frac{\sigma_{x}+\sigma_{y}}{2} \right )^{2}=\left ( \frac{\sigma_{x}-\sigma_{y}}{2}\cos 2\theta \right )^{2}+2\left ( \frac{\sigma_{x}-\sigma_{y}}{2}\cos 2\theta  \right )\left ( \tau_{xy}\sin 2\theta \right )+\left ( \tau_{xy}\sin 2\theta \right )^{2}$

 

$\left ( \tau_{x'y'} \right )^{2}=\left ( -\frac{\sigma_{x}-\sigma_{y}}{2}\sin 2\theta \right )^{2}-2\left (\frac{\sigma_{x}-\sigma_{y}}{2}\sin 2\theta \right )\left ( \tau_{xy} \cos 2\theta \right )+\left ( \tau_{xy} \cos 2\theta \right )^{2}$

 

두 식의 각 변을 더해줍니다. 

 

$\left ( \sigma_{x'}-\frac{\sigma_{x}+\sigma_{y}}{2} \right )^{2}+\left ( \tau_{x'y'} \right )^{2}=\left (\frac{\sigma_{x}-\sigma_{y}}{2}\right )^{2}\left ( \sin^{2} 2\theta+\cos^{2} 2\theta \right )+\left ( \tau_{xy}  \right )^{2}\left ( \sin^{2} 2\theta+\cos^{2} 2\theta \right )$

 

$\left ( \sin^{2} 2\theta+\cos^{2} 2\theta \right )$ 이 1이므로 위 식은 아래와 같이 변형됩니다. 

 

$\left ( \sigma_{x'}-\frac{\sigma_{x}+\sigma_{y}}{2} \right )^{2}+\left ( \tau_{x'y'} \right )^{2}=\left (\frac{\sigma_{x}-\sigma_{y}}{2}\right )^{2}+\left ( \tau_{xy}  \right )^{2}$

 

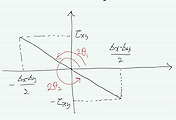
모어원 공식이 유도되었습니다. 그리는 방법은 다음시간에 알아봅시다.