[재료역학] 평면응력 (3) 최대전단응력공식 유도

지난 글에서 유도한 응력의 변환방정식은 아래와 같습니다. 

$\sigma_{x'}=\frac{\sigma_{x}+\sigma_{y}}{2}+\frac{\sigma_{x}-\sigma_{y}}{2}\cos 2\theta+\tau_{xy}\sin 2\theta$

$\tau_{x'y'}=-\frac{\sigma_{x}-\sigma_{y}}{2}\sin 2\theta+\tau_{xy} \cos 2\theta$

 

최대전단응력공식을 유도할때는 두번째 식이 사용됩니다. 변수는 $\theta$ 입니다. $\theta$로 미분한 함수가 0이 되는 $\theta$ 에서 극값이 발생합니다. 

 

두번째 식을 $\theta$ 로 미분하면 아래와 같습니다. 

 

$\frac{d\sigma_{x'}}{d \theta}=-(\sigma_{x}-\sigma_{y})\cos 2\theta-2\tau_{xy}\sin 2\theta=0$

아래와 같이 변형합니다. 

$\frac{\sin 2\theta}{\cos 2\theta}=-\frac{ \frac{(\sigma_{x}-\sigma_{y})}{2}   }{\tau_{xy}    }$

 

좌변은 탄젠트입니다.

 

$\tan 2\theta=-\frac{ \frac{(\sigma_{x}-\sigma_{y})}{2}   }{\tau_{xy}}$

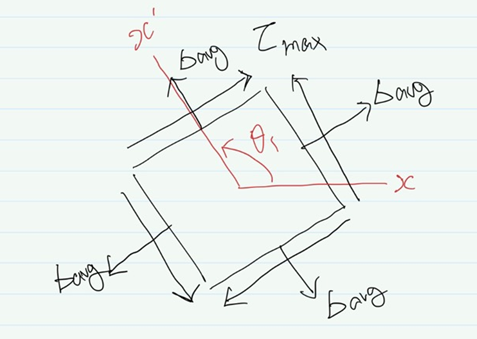
위 등식을 만족하는 $\theta$ 를 구할 필요는 없습니다. 아래그림의 $\theta_{1}$과 $\theta_{2}$가 위 등식이 만족한다는 것을 알면 됩니다. (어떤 교제는 다른 방식으로 각도를 잡기도 합니다. 결과는 같습니다.)

 

 

또한 $\theta_{1}$과 $\theta_{2}$는 90도 차이임을 알 수 있습니다. 

$\theta=\theta_{1}$일 때 전단응력의 변환방정식은 아래와 같이 변형됩니다. 위 그림에서 $\sin 2\theta_{1}$과 $\cos 2\theta_{1}$을 구하여 넣어주었습니다. 

$\tau_{max}=-\frac{\sigma_{x}-\sigma_{y}}{2}
\frac{\frac{\sigma_{x}-\sigma_{y}}{2}}{\sqrt{\left ( \frac{\sigma_{x}-\sigma_{y}}{2} \right )^{2}+\tau_{xy}^{2}}}
+\tau_{xy}
\frac{-\tau_{xy}}{\sqrt{\left ( \frac{\sigma_{x}-\sigma_{y}}{2} \right )^{2}+\tau_{xy}^{2}}}$

 

아래와 같이 계산해줍니다. 

 

$\tau_{max}=-
\frac{ \left (\frac{\sigma_{x}-\sigma_{y}}{2}  \right )^{2}+\tau_{xy}^{2} }{\sqrt{\left ( \frac{\sigma_{x}-\sigma_{y}}{2} \right )^{2}+\tau_{xy}^{2}}}$

 

아래와 같이 변형합니다. 

 

$\tau_{max}=-\sqrt{\left ( \frac{\sigma_{x}-\sigma_{y}}{2} \right )^{2}+\tau_{xy}^{2}}$

 

$\theta=\theta_{2}$일 때도 같은 방법으로 구하면 아래와 같습니다. 

 

$\tau_{max}=\sqrt{\left ( \frac{\sigma_{x}-\sigma_{y}}{2} \right )^{2}+\tau_{xy}^{2}}$

 

부호규약을 적용하여 최대전단응력만 나타내면 아래와 같습니다. 

 

 

최대전단응력 상태에서 수직응력은 어떤 값을 가질까요? $\theta_{1}$과 $\theta_{2}$에서 수직응력을 구하면 아래와 같습니다. 수직응력변형공식에 위에서 구한 사인과 코사인 값을 대입해서 구하면 됩니다.

 

$\sigma_{x'}=\frac{\sigma_{x}+\sigma_{y}}{2}$

 

$\sigma_{y'}=\frac{\sigma_{x}+\sigma_{y}}{2}$

 

 위 응력은 x방향과 y방향의 평균응력입니다. $\sigma_{avg}$라고 부릅니다. 따라서 최대전단응력상태에서 요소는 아래와 같이 나타낼 수 있습니다. 

 

 

이번에는 주응력과의 관계를 알아봅시다. 주응력이 발생하는 각도는 아래와 같습니다. 

 

$\tan 2\theta=\frac{\tau_{xy}}{\frac{(\sigma_{x}-\sigma_{y})}{2}}$

 

최대 전단응력이 발생하는 각도는 아래와 같습니다. 

 

$\tan 2\theta=\frac{\tau_{xy}}{\frac{(\sigma_{x}-\sigma_{y})}{2}}$

 

탄젠트값의 부호가 다르다는 것은 90도 차이임을 의미합니다. $2\theta$가 90도 차이이므로 $\theta$는 45도 차이입니다. 

---

아래는 요약입니다. 

 

1. 최대전단응력은 전단응력 변환공식을 미분한 값이 0이 될 때 발생하며, 발생 각도와 최대전단응력은 아래와 같다.

 

$\tan 2\theta=-\frac{ \frac{(\sigma_{x}-\sigma_{y})}{2}   }{\tau_{xy}}$

 

$\tau_{max}=-\sqrt{\left ( \frac{\sigma_{x}-\sigma_{y}}{2} \right )^{2}+\tau_{xy}^{2}}$   (at $\theta_{1}$)

 

$\tau_{max}=\sqrt{\left ( \frac{\sigma_{x}-\sigma_{y}}{2} \right )^{2}+\tau_{xy}^{2}}$   (at $\theta_{2}$)

 

2. $\theta_{1}$과 $\theta_{2}$는 90도 차이이고, 최대전단응력상태에서 주응력은 $\sigma_{avg}$ 이므로 아래와 같이 나타낼 수 있다.