3차원 곡선 위의 한 점에서 법선(normal)방향의 단위벡터와 접선(tangent) 방향의 단위벡터를 정의할 수 있습니다. 기호로 아래와 같이 나타냅니다.
단위 법선 벡터 : $\vec{e}_{n}$
단위 접선 벡터 : $\vec{e}_{t}$
그림으로 나타내면 아래와 같습니다.
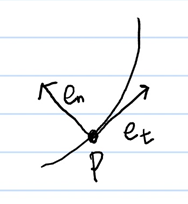
점 P가 P'으로 이동했다고 합시다. 이동한 P'의 접선벡터를 $\vec{e}'_{t}$라고 놓겠습니다.
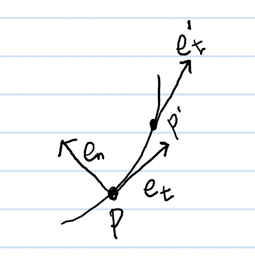
아래 그림과 같이 두 점 사이의 변위벡터를 $\Delta \vec{e}_{t}$ 라고 놓겠습니다.

$\vec{e}'_{t}$ 와 $\vec{e}_{t}$ 를 따로 그리면 아래와 같습니다. 사이 각도는 $\Delta \theta$로 놓겠습니다.

$\Delta \vec{e}_{t}$ 는 아래와 같이 표현됩니다.
$\Delta \vec{e}_{t}=\vec{e}'_{t}-\vec{e}_{t}$
크기와 단위방향벡터로 나타내면 아래와 같습니다.
$\Delta \vec{e}_{t}=2\sin \frac{\Delta \theta}{2} \cdot \frac{\vec{e}'_{t}-\vec{e}_{t}}{\left | \vec{e}'_{t}-\vec{e}_{t} \right |}$
양변에 극한을 취해줍니다.
$\lim_{\Delta \theta \rightarrow 0} \Delta \vec{e}_{t}=\lim_{\Delta \theta \rightarrow 0} 2\sin \frac{\Delta \theta}{2} \cdot \frac{\vec{e}'_{t}-\vec{e}_{t}}{\left | \vec{e}'_{t}-\vec{e}_{t} \right |}$
우변의 첫항은 1로 수렴하고, 두번째 항은 $\vec{e}_{n}$으로 수렴합니다.
$\lim_{\Delta \theta \rightarrow 0} \Delta \vec{e}_{t}=\vec{e}_{n}$
좌변은 아래와 같이 쓸 수 있습니다.
$\frac{d \vec{e}_{t}}{d \theta}=\vec{e}_{n}$
단위 법선벡터와 단위 접선벡터 사이의 관계식이 유도되었습니다.
'동역학 > OLD' 카테고리의 다른 글
| [동역학] 13. 곡선위를 움직이는 점의 순간속도와 순간가속도를 법선벡터와 접선벡터로 나타내기 (0) | 2022.04.11 |
|---|---|
| [동역학] 입자의 곡선운동 예제 : 포물선 운동 (0) | 2021.07.23 |
| [동역학] 3차원에서 입자의 곡선운동 (0) | 2021.07.23 |
| [동역학] 가속도가 일정한 경우의 1차원 운동(위치,속도) (0) | 2021.07.22 |
| [동역학] 속도가 일정한 경우의 1차원 운동(위치,가속도) (0) | 2021.07.22 |
댓글