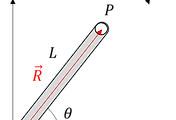
아래 그림과 같이 4절 크랭크-슬라이더가 있습니다. 주어진 값은 각 링크의 길이인 $L_{2}$,$L_{3}$,$L_{4}$와 $\theta_{2}$ 입니다. 이 값들을 이용하여 $\theta_{3}$ 와 L1을 구하는 것이 목적입니다.

벡터 방정식은 아래와 같습니다.
$\vec{R}_{2}=\vec{R}_{1}+\vec{R}_{4}+\vec{R}_{3}$
아래와 같이 이항합시다.
$\vec{R}_{2}-\vec{R}_{1}-\vec{R}_{4}-\vec{R}_{3}=0$
오일러 공식을 이용하여 복소평면의 극좌표로 변형하면 아래와같습니다.
$L_{2}e^{j\theta_{2}}-L_{1}e^{j\theta_{1}}-L_{4}e^{j\theta_{4}}-L_{3}e^{j\theta_{3}}=0$
사인,코사인 형태로 나타내면 아래와 같습니다.
$L_{2}\left ( \cos \theta_{2}+j\sin \theta_{2} \right )
-L_{1}\left ( \cos \theta_{1}+j\sin \theta_{1} \right )
-L_{4}\left ( \cos \theta_{4}+j\sin \theta_{4} \right )
-L_{3}\left ( \cos \theta_{3}+j\sin \theta_{3} \right )=0$
$\theta_{1}$은 0도이므로, 아래와 같이 변형됩니다.
$L_{2}\left ( \cos \theta_{2}+j\sin \theta_{2} \right )
-L_{1}
-L_{4}\left ( \cos \theta_{4}+j\sin \theta_{4} \right )
-L_{3}\left ( \cos \theta_{3}+j\sin \theta_{3} \right )=0$
$\theta_{4}$은 90도이므로, 아래와 같이 변형됩니다.
$L_{2}\left ( \cos \theta_{2}+j\sin \theta_{2} \right )
-L_{1}
-L_{4}j
-L_{3}\left ( \cos \theta_{3}+j\sin \theta_{3} \right )=0$
실수부와 허수부를 나눠서 써줍니다.
$L_{2}\cos\theta_{2}
-L_{1}
-L_{3}\cos \theta_{3}
=0$
$L_{2}\sin\theta_{2}
-L_{4}
-L_{3}\sin \theta_{3}
=0$
두번째 식을 이용하여 $\theta_{3}$를 구하면 아래와 같습니다.
$\theta_{3}=sin^{-1}\left ( \frac{L_2\sin\theta_{2}-L_{4}}{L_{3}} \right )$
첫번쨰 식을 이용하여 $L_{1}$을 구하면 아래와 같습니다.
$L_{1}=L_{2}\cos\theta_{2}-L_{3}\cos \theta_{3}$
주의할 점이 하나 있습니다. 같은 양의 $y$값을 갖는 $\theta$가 두개 있다는 것입니다.

이를 유념하여, 두 $\theta$를 모두 구해야 합니다. 두 값의 합은 $\pi$ 이므로 한 값을 구하고 나서 $\pi$에서 빼주면 나머지 값이 구해집니다.
'기계공학 기타과목 > 기구학' 카테고리의 다른 글
| [기구학] 한 끝이 고정된 링크의 속도벡터 구하기 (0) | 2022.06.30 |
|---|---|
| [기구학] 4절 크랭크-슬라이더 위치해석 (position analysis) (2) 파이썬으로 위치계산기 만들기 (0) | 2022.06.28 |
| [기구학] 4절 링크 위치해석 (position analysis) (2) 파이썬으로 위치계산기 만들기 (0) | 2022.06.27 |
| [기구학] 4절 링크 위치해석 (position analysis) (1) 공식 유도 (0) | 2022.06.23 |
| [가구학] 평면운동기구 자유도 구하는 원리 설명 (그뤼블러 판별식) (0) | 2022.06.08 |

댓글