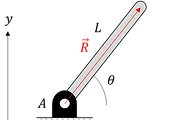
아래와 같이 링크가 하나 있다고 합니다.

우리는 끝단 P에서의 속도를 구하고 싶은 상황입니다. 알고 있는 것은 L,θ,ω 입니다.
1. 위치벡터
끝단 P의 위치벡터를 아래와 같이 표현할 수 있습니다.
→R=Lejθ
2. 속도벡터
양면을 t로 미분하면 끝단의 속도벡터가 됩니다.
→V=d→Rdt=dLejθdt
상수 L을 앞으로 꺼내줍니다.
→V=d→Rdt=Ldejθdt
체인룰을 적용합니다.
→V=d→Rdt=Ldejθdθdθdt
우변 두번째 인수를 미분하면 아래와 같습니다.
→V=d→Rdt=Ljejθdθdt
우변 세번째 인수는 각속도 오메가입니다.
→V=d→Rdt=Ljejθω
아래와 같이 바꿔씁니다.
→V=d→Rdt=Lωejθj
위치벡터 →R에서 ωj가 곱해졌습니다. 속도벡터의 크기는 |Lω| 입니다. 방향을 알아야 하는데요. Lejθ 에 ωj 가 곱해진 방향입니다. 복소좌표계에서 j를 곱하는 것의 의미를 알아봅시다.
3. 복소좌표계에서 j를 곱한다는 것은?
(1,0)의 위치벡터를 복소수로 표현하면 아래와 같습니다.
1+0j
j를 곱하면 아래와 같습니다.
0+j
그림으로 나타내면 아래와 같습니다.

j를 곱하면 반시계방향으로 90도 회전합니다. 반대로 -j 를 곱하면 시계방향으로 90도 회전합니다.
4. 속도벡터의 방향
위에서 구한 속도 벡터 수식을 다시 봅시다.
→V=d→Rdt=Lωejθj
속도벡터는 ejθ 에서 90도 회전한 방향으로 작용합니다. 시계방향인지 반시계방향인지는 오메가의 부호가 결정합니다. 오메가의 부호가 양수이면 (+j)가 곱해지는 것이므로, 반시계방향으로 90도 회전한 방향으로 작용합니다. 오메가의 부호가 음수라고 가정하고 속도벡터를 그림으로 나타내면 아래와 같습니다.

'기계공학 기타과목 > 기구학' 카테고리의 다른 글
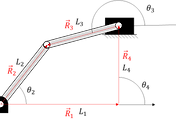
| [기구학] 4절 링크 위치해석 (position analysis) (1) 도해법 (0) | 2022.07.04 |
|---|---|
| [기구학] 움직이는 링크의 속도벡터 구하기 (0) | 2022.06.30 |
| [기구학] 4절 크랭크-슬라이더 위치해석 (position analysis) (2) 파이썬으로 위치계산기 만들기 (0) | 2022.06.28 |
| [기구학] 4절 크랭크-슬라이더 위치해석 (position analysis) (1) 공식 유도 (0) | 2022.06.27 |
| [기구학] 4절 링크 위치해석 (position analysis) (2) 파이썬으로 위치계산기 만들기 (0) | 2022.06.27 |

댓글