[재료역학] 평면응력 (7) 모어원 그려보기

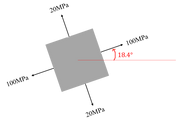
우리는 아래 응력상태에서 응력 변환공식을 유도했고, 응력변환공식을 이용해서 모어원을 유도했습니다. 

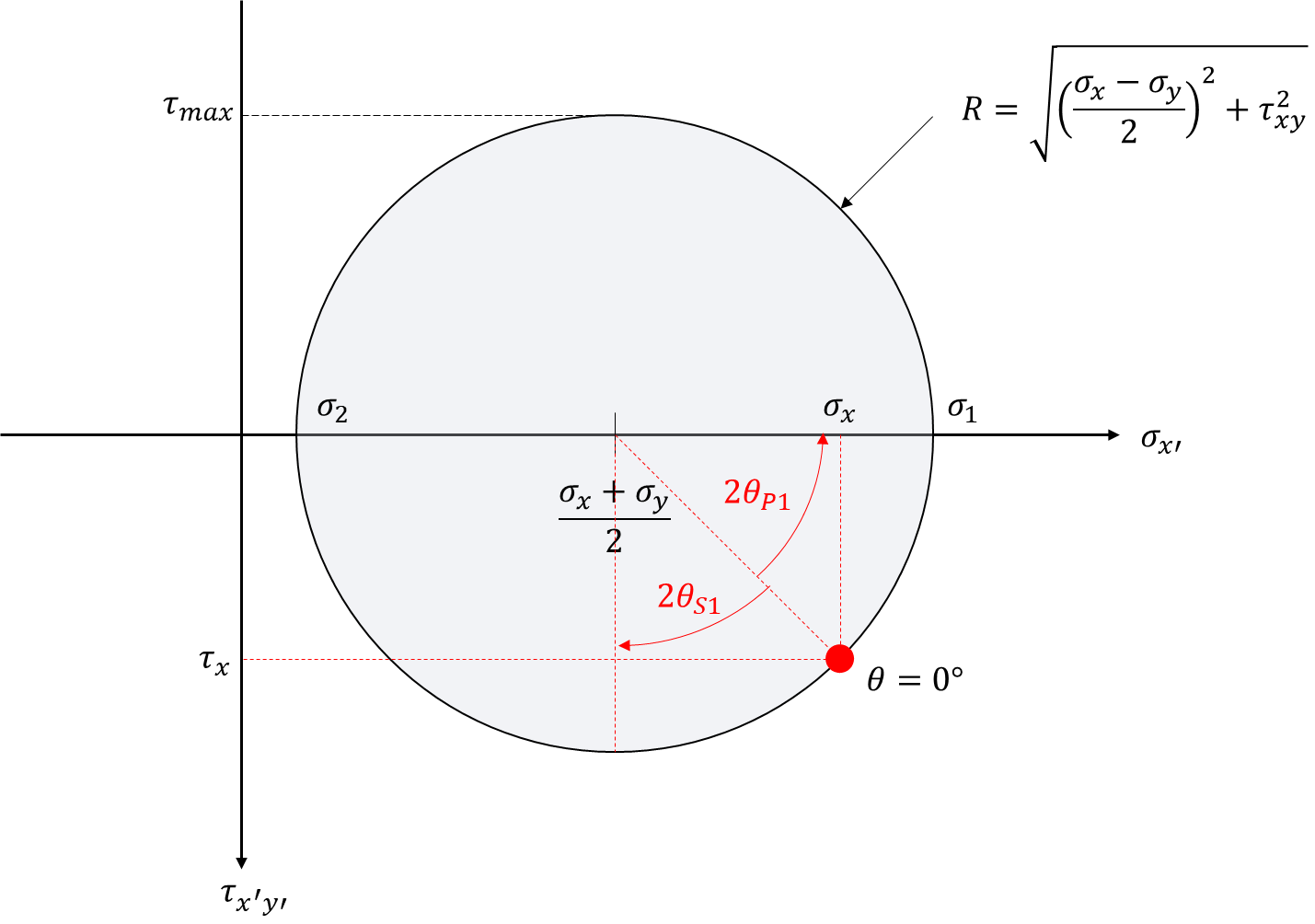
지난시간에 유도한 모어원 수식은 아래와 같습니다. 

 

$\left ( \sigma_{x'}-\frac{\sigma_{x}+\sigma_{y}}{2} \right )^{2}+\left ( \tau_{x'y'} \right )^{2}=\left (\frac{\sigma_{x}-\sigma_{y}}{2}\right )^{2}+\left ( \tau_{xy}  \right )^{2}$

 

원을 그려볼 것인데요. 먼저 축을 알아야 합니다. 일반적으로 x축과 y축을 사용합니다. 변수 x와 y가 사용되었기 때문입니다. 위 식에서 변수는 $\sigma_{x'}$  와 $\tau_{x'y'}$  입니다. 따라서 축은 아래와 같이 그려집니다. 모어원을 그릴 때 y축은 아래쪽을 (+) 방향

 

 

원은 중심과 반지름만 알면 그릴 수 있습니다. 원의 중심의 좌표와 반지름은 아래와 같습니다. 

 

중심 좌표 = $\left ( \frac{\sigma_{x}+\sigma_{y}}{2},0 \right )$ 

 

반지름 = $\sqrt{\left (\frac{\sigma_{x}-\sigma_{y}}{2}\right )^{2}+\left ( \tau_{xy}  \right )^{2}}$

 

반지름은 최대전단응력과 같습니다. 

 

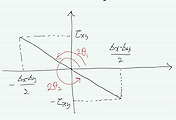
모오원을 그리면 아래와 같습니다. 

 

 

 

x축과 만나는 두 점은 수직응력의 최댓값과 최솟값입니다. 최대주응력입니다. 아래와 같이 표시해줍시다. 

 

 

 

0도를 찾아주어야 합니다. 0도 일 때의 응력은 $\sigma_{x}$ , $\sigma_{y}$ , $\tau_{xy}$ 입니다. 표시해줍니다.  

 

 

주응력과 최대전단응력의 각도를 표시해줍니다.