아래와 같이 스프링이 직렬 및 병렬연결되어 있습니다.
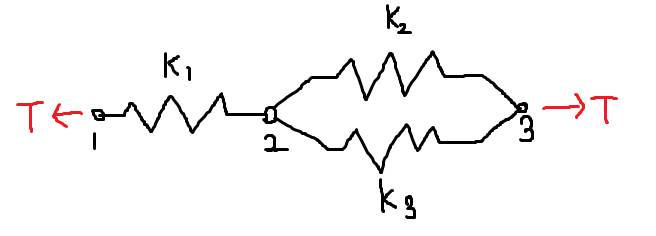
양 쪽에 T라는 힘이 작용하고 있습니다. 각 노드에서의 변위를 $ 라고 놓겠습니다.
각 요소의 힘-변위 방정식 구하기
스프링 1에서의 힘-변위 방정식은 아래와 같습니다. 하중에서 위 첨자는 스프링번호, 아래첨자는 노드번호입니다.
$\begin{bmatrix}
f^{(1)}_{1}\\
f^{(1)}_{2}
\end{bmatrix}
=
\begin{bmatrix}
k_{1} &-k_{1} \\
-k_{1} &k_{1}
\end{bmatrix}\begin{bmatrix}
u_{1}\\
u_{2}
\end{bmatrix}$
스프링 2에서의 힘-변위 방정식은 아래와 같습니다.
$\begin{bmatrix}
f^{(2)}_{2}\\
f^{(2)}_{3}
\end{bmatrix}
=
\begin{bmatrix}
k_{2} &-k_{2} \\
-k_{2} &k_{2}
\end{bmatrix}\begin{bmatrix}
u_{2}\\
u_{3}
\end{bmatrix}$
스프링 3에서의 힘-변위 방정식은 아래와 같습니다.
$\begin{bmatrix}
f^{(3)}_{2}\\
f^{(3)}_{3}
\end{bmatrix}
=
\begin{bmatrix}
k_{3} &-k_{3} \\
-k_{3} &k_{3}
\end{bmatrix}\begin{bmatrix}
u_{2}\\
u_{2}
\end{bmatrix}$
스프링 2와 3의 힘-변위방정식을 더해주면 아래와 같습니다.
$\begin{bmatrix}
f^{(2)}_{2}+f^{(3)}_{2}\\
f^{(3)}_{3}+f^{(3)}_{3}
\end{bmatrix}
=
\begin{bmatrix}
k_{2}+k_{3} &-(k_{2}+k_{3}) \\
-(k_{2}+k_{3}) & k_{2}+k_{3}
\end{bmatrix}\begin{bmatrix}
u_{2}\\
u_{3}
\end{bmatrix}$
스프링1의 힘-변위 방정식과 합쳐줍시다.
$\begin{bmatrix}
f^{(1)}_{1}\\
f^{(1)}_{2}+f^{(2)}_{2}+f^{(3)}_{2}\\
f^{(2)}_{3}+f^{(3)}_{3}
\end{bmatrix}=\begin{bmatrix}
k_{1} & -k_{1} & 0 \\
-k_{1} & k_{1}+k_{2}+k_{3} & -(k_{2}+k_{3}) \\
0 & -(k_{2}+k_{3}) & k_{2}+k_{3}
\end{bmatrix}
\begin{bmatrix}
u_{1}\\
u_{2}\\
u_{3}
\end{bmatrix}$
변위구하기
위 수식에서 각 노드에 가해진 힘을 계산하면 아래와 같습니다 .
$\begin{bmatrix}
-T\\
0\\
T
\end{bmatrix}=\begin{bmatrix}
k_{1} & -k_{1} & 0 \\
-k_{1} & k_{1}+k_{2}+k_{3} & -(k_{2}+k_{3}) \\
0 & -(k_{2}+k_{3}) & k_{2}+k_{3}
\end{bmatrix}
\begin{bmatrix}
u_{1}\\
u_{2}\\
u_{3}
\end{bmatrix}$
양변에 역행렬을 곱해서 변위를 구하면 됩니다.
'기계공학 기타과목 > 유한요소해석 강의' 카테고리의 다른 글
| [유한요소법] 6. 강성행렬 감잡기 (7) 직렬스프링+끝단고정 (0) | 2022.03.31 |
|---|---|
| [유한요소법] 6. 강성행렬 감잡기 (6) 직렬 스프링 2개 예제 (0) | 2021.06.15 |
| [유한요소법] 6. 강성행렬 감잡기 (4) 스프링 직렬연결 중첩규칙 (0) | 2021.06.08 |
| [유한요소법] 6. 강성행렬 감잡기 (3) 선형 스프링 3개 직렬 (0) | 2021.06.08 |
| [유한요소법] 6. 강성행렬 감잡기 (2) 선형 스프링 2개 직렬 (2) | 2021.06.04 |




댓글