[손으로 푸는 재료역학] 2. 응력이란 무엇인가 (1) 2차원

먼저 과거 선배들이 응력을 생각해내게 된 동기(motivation)를 생각해봅시다. 어떤 물체에 힘을 가할 때, 힘을 계속 증가시키다 보면 물체가 변형되다가 파손됩니다. 파손되는 위치는 아마 가장 취약한 부분일텐데요. 이 취약한 위치를 찾아내려면 물체 내부의 각 위치가 받는 힘을 정의해야 했을 것입니다. 물체 내부의 각 위치는 물체를 연속체로 생각했을 때, 물체 내부의 한 점 (x,y,z) 을 의미합니다. 물체 내부의 각 위치에 가해지는 힘을 찾는 과정에서 응력이 발견되었을 것이라 생각합니다. 

 

응력에 익숙해질 수는 있지만 직관적으로 이해하기는 어렵다는 것을 알고 시작합시다. 점에 가해지는 힘이라는 것을 받아들이기 어렵고, 한 점에 가해지는 힘이 9개나 된다는 것은 더 이해하기 어렵습니다. 

 

먼저 2차원에서 응력을 이해하고, 다음 글에서 3차원 응력을 다루겠습니다. 

 

2차원에 놓인 물체에 하중이 가해지고 있다고 합시다. 

 

물체 내부의 작은 사각형 모양의 영역을 하나 잡아봅시다.

 

 

사각형의 각 변에는 힘이 작용하고 있을 것입니다. 더 정확히는 각 변 위의 위치마다 힘이 다르게 작용하고 있을 것이지만, 각 변에 작용하는 평균힘을 생각합시다. 먼저 윗변에 작용하는 힘을 알아봅시다. 힘은 기울어진 임의 방향으로 작용하고 있을 것입니다. 

 

 

2차원이므로, 힘을 두 방향으로 분해할 수 있습니다. 아래와 같습니다. 

 

 

나머지 면에도 힘이 가해지고 있습니다. 각 면에 가해진 힘을  아래와 같이  표시할 수 있습니다. 재료역학은 정적(static)상태를 가정하므로,  $\sum F=0$, $\sum M=0$  이 되도록 놓은 것입니다. $F_{xy}$ 와 $F_{xy}$는 전단력이고 둘의 크기가 같습니다. 

 

 

(위 그림을 보시고 그런가보다 하는 분들도 있고, 왜 이런지 궁금하신 분들도 있을텐데요. 위와 같은 하중 상태의 유일성은 다다음 글에서 보이겠습니다.)

 

의미를 이해해봅시다. $F_{xy}$ 에서 앞에 붙어있는 x는 x방향을 법선으로 하는 변을 의미합니다. 뒤에 붙어있는 y는 힘이 가해지는 방향입니다. 따라서 $F_{xy}$ 는 x를 법선으로 하는 변에 작용하고 방향은 y인 전단력을 의미합니다. 

 

이제 각 변의 길이를 줄여봅시다. 변의 길이가 0이 되면 한 점이 되고, 힘도 0이 됩니다. 점에서의 힘을 정의할 수가 없습니다. 하지만 아래와 같이 힘과 변 길이의 비율을 정의하면 이야기가 달라집니다. 한 변의 길이를 $\Delta l$ 이라고 놓겠습니다. 힘을 길이로 나눈 값의 극한이 수렴합니다. 

 

$\lim_{\Delta l\rightarrow 0}\frac{F_{y}}{l}$

 

$\lim_{\Delta l\rightarrow 0}\frac{F_{x}}{l}$

 

$\lim_{\Delta l\rightarrow 0}\frac{F_{xy}}{l}$

 

$\lim_{\Delta l\rightarrow 0}\frac{F_{xy}}{l}$

 

극한값을 응력이라고 부릅니다. 기호로는 아래와 같이 나타냅니다. 

 

$\lim_{\Delta l\rightarrow 0}\frac{F_{y}}{l}=\sigma_{y}$

 

$\lim_{\Delta l\rightarrow 0}\frac{F_{x}}{l}=\sigma_{x}$

 

$\lim_{\Delta l\rightarrow 0}\frac{F_{xy}}{l}=\tau_{xy}$

 

$\lim_{\Delta l\rightarrow 0}\frac{F_{xy}}{l}=\tau_{yx}$

 

$\sigma_{y}$ 와 $\sigma_{x}$ 는 수직응력이라고 부릅니다. $\tau_{xy}$ 와 $\tau_{yx}$ 는 전단응력이라고 부르고 크기가 같습니다. 그림으로 나타내면 아래와 같습니다. 

 

 

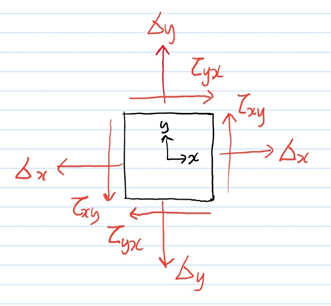
크기가 같은 힘을 생략하고 간단히 나타내면 아래와 같습니다. 

 

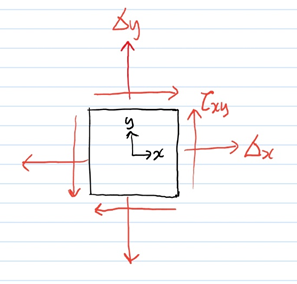
마치 넓이가 있는 사각형에 응력이 작용하고 있는 것과 같은 그림이지만, 응력은 점에 작용합니다. 위 그림은 점을 확대한 모습이라고 생각하시면 됩니다. 사실 점은 확대해도 면적이 없긴한데, 인간이 볼 수 있게 표현한 것이라고 생각합시다. 점 하나에 네가지 응력이 작용하고 있는 것입니다. 직관적으로 이해하기 어렵습니다. 

 

2차원에서 점 하나에 작용하는 물리량을 떠올려봅시다. 질량이 있을겁니다. 질량은 1개의 요소만 갖습니다. 질량은 스칼라입니다. 다른 물리량으로는 속도와 가속도도 있습니다. 2차원에서 속도와 가속도는 x방향, y방향 두개의 요소를 갖습니다. 벡터입니다. 2차원에서 응력은 4개의 요소($\sigma_{x}$,$\sigma_{y}$,$\tau_{xy}$,$\tau_{yx}$) 를 갖습니다. 벡터를 넘어섭니다. 이를 텐서라고 합니다. 스칼라와 벡터도 텐서의 일종인데 네번째 글에서 다루겠습니다.